Hãy chứng minh rằng
a) Hàm số \(y = \sqrt {2x - {x^2}} \) nghịch biến trên đoạn [1;2]
b) Hàm số \(y = \sqrt {{x^2} - 9} \) đồng biến trên nửa khoảng \({\rm{[}}3; + \infty )\)
c) Hàm số \(y = x + {4 \over x}\) nghịch biến trên mỗi nửa khoảng [-2;0) và (0;2]
Giải
a) Hàm số liên tục trên đoạn [1;2] và có đạo hàm
\(y’ = {{1 - x} \over {\sqrt {2x - {x^2}} }} < 0\) với mọi \(x \in (1,2)\)
Do đó hàm số nghịch biến trên đoạn [1;2]
b) Hàm số liên tục trên nửa khoảng \({\rm{[}}3; + \infty )\) và có đạo hàm
Advertisements (Quảng cáo)
\(y’ = {x \over {\sqrt {{x^2} - 9} }} > 0\) với mọi \(x \in (3, + \infty )\)
Do đó hàm dố đồng biến tên nửa khoảng \({\rm{[}}3; + \infty )\)
c) TXĐ: \(x\ne0\)
\(y’ = 1 - {4 \over {{x^2}}}\)
\(y’ = 0 \Leftrightarrow x = \pm 2\)
BBT
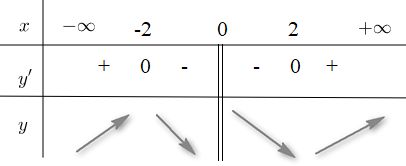
Từ BBT ta có hàm số \(y = x + {4 \over x}\) nghịch biến trên mỗi nửa khoảng [-2;0) và (0;2]
