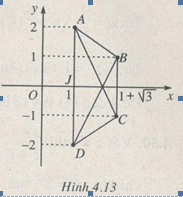
Cho A, B, C, D là bốn điểm trong mặt phẳng phức theo thứ tự biểu diễn các số
\(1 + 2i\), \(1 + \sqrt 3 + i\), \(1 + \sqrt 3 - i\), \(1 - 2i\)
Chứng minh rằng ABCD là một tứ giác nội tiếp đường tròn. Hỏi tâm đường tròn đó biểu diễn số phức nào ?
Giải
Advertisements (Quảng cáo)
Vì mỗi cặp số \(1 + 2i\), \(1 - 2i\) và \(1 + \sqrt 3 + i\), \(1 + \sqrt 3 - i\) là cặp số phức liên hợp nên hai điểm A, D, hai điểm B, C đối xứng qua \(Ox\); phần thực của hai số đầu khác phần thực của hai số sau nên ABCD là một hình thang cân , do đó nó là một tứ giác nội tiếp đường tròn có tâm J nằm trên trục đối xứng \(Ox\); J biểu diễn số thực \(x\) sao cho \(\left| {\overrightarrow {JA} } \right| = \overrightarrow {\left| {JB} \right|} \Leftrightarrow \left| {1 - x + 2i} \right| = \left| {1 - x + \sqrt 3 + i} \right|\). Từ đó suy ra \(x\) = 1.
(Cách khác : \(\overrightarrow {AB} \) biểu diễn số phức \( \sqrt 3 - i\), \(\overrightarrow {DB} \) biểu diễn số phức \(\sqrt 3 + 3i\) mà \({{\sqrt 3 + 3i} \over {\sqrt 3 - i}} = \sqrt 3 i\) nên \(\overrightarrow {AB} \overrightarrow {.DB} = 0\). Tương tự (hay vì lí do đối xứng qua \(Ox\)), \(\overrightarrow {DC} .\overrightarrow {AC} = 0\). Từ đó suy ra AD là một đường kính của đường tròn đi qua A, B, C, D . ( h.4.13)