Gọi M, M’ theo thứ tự là các điểm của mặt phẳng phức biểu diễn số . Câu 4.6 trang 177 sách bài tập Giải tích 12 Nâng cao - Bài 1. Số phức
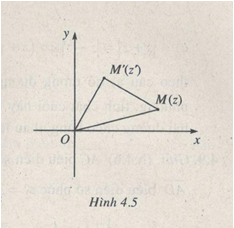
Gọi M, M’ theo thứ tự là các điểm của mặt phẳng phức biểu diễn số \(z \ne 0\) và \(z’ = {{1 + i} \over 2}z\). Chứng minh rằng tam giác OMM’ là tam giác vuông cân (O là gốc tọa độ)
Giải
Ta có \(\left| {\overline {OM} } \right| = \left| z \right|,\)
Advertisements (Quảng cáo)
\(\eqalign{& \left| {\overline {OM’} } \right| = \left| {{{1 + i} \over 2}} \right|\left| z \right| = {{\sqrt 2 } \over 2}\left| z \right| \cr & \left| {\overline {MM’} } \right| = \left| {\overline {OM’} - \overline {OM} } \right| = \left| {{{ - 1 + i} \over 2}} \right|\left| z \right| = {{\sqrt 2 } \over 2}\left| z \right| \cr} \)
Do \(\left| z \right| \ne 0,\) suy ra tam giác OMM’ là tam giác vuông cân đỉnh M’ (h.4.5)
