
Tính các góc của tứ giác trong hình 36:
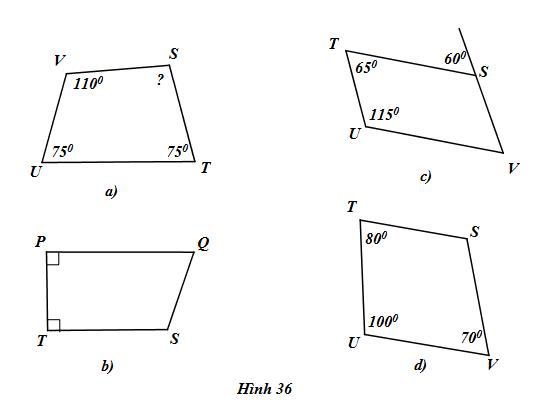

a) Tứ giác UVST có: \(\widehat U + \widehat V + \widehat T + \widehat S = {360^0}\)
Do đó: \({75^0} + {110^0} + {75^0} + \widehat S = {360^0}\)
\( \Rightarrow \widehat S = {360^0} - \left( {{{75}^0} + {{110}^0} + {{75}^0}} \right) = {360^0} - {260^0} = {100^0}\)
b) Tứ giác TPQS có \(\widehat T + \widehat P + \widehat Q + \widehat S = {360^0}\)
Do đó: \({90^0} + {90^0} + {70^0} + \widehat S = {360^0}\)
Advertisements (Quảng cáo)
\( \Rightarrow \widehat S = {360^0} - \left( {{{90}^0} + {{90}^0} + {{70}^0}} \right) = {360^0} - {250^0} = {110^0}\)
c) Tứ giác TUVS có: \(\widehat T + \widehat U + \widehat V + \widehat S = {360^0}\)
Do đó: \({65^0} + {115^0} + {60^0} + \widehat S = {360^0}\)
\( \Rightarrow \widehat S = {360^0} - \left( {{{65}^0} + {{115}^0} + {{60}^0}} \right) = {360^0} - {240^0} = {120^0}\)
d) Tứ giác TURS có: \(\widehat T + \widehat U + \widehat R + \widehat S = {360^0}\)
Do đó: \({80^0} + {100^0} + {70^0} + \widehat S = {360^0}\)
\( \Rightarrow \widehat S = {360^0} - \left( {{{80}^0} + {{100}^0} + {{70}^0}} \right) = {360^0} - {240^0} = {110^0}\)
