
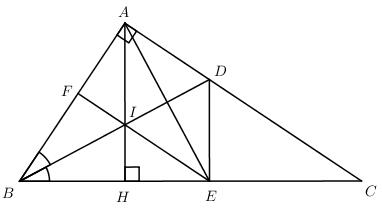
Cho tam giác ABC vuông tại A (AB < AC). Tia phân giác của góc B cắt AC tại D. Trên BC lấy điểm E sao cho BE = BA.
a) Chứng minh rằng: \(\Delta ABD = \Delta EBD\) .
b) Kẻ đường cao AH của tam giác ABC. Chứng mình rằng tứ giác ADEH là hình thang vuông.
c) Gọi I là giao điểm của AH với BD, đường thẳng EI cắt AB tại F. Chứng minh rằng tứ giác ACEF là hình thang vuông.

a) Xét \(\Delta ABD\) và \(\Delta EBD\) ta có:
\(AB = BE\,\,\left( {gt} \right)\)
BD là cạnh chung
\(\widehat {ABD} = \widehat {DBE}\) (BD là tia phân giác của góc B)
Do đó \(\Delta ABD = \Delta EBD\,\,\left( {c.g.c} \right)\)
b) Ta có : \(\widehat {DEB} = \widehat {BAD}\,\,\left( {\Delta EBD = \Delta ABD} \right)\)
Mà \(\widehat {BAD} = {90^0}\) (\(\Delta ABD\) vuông tại A)
Advertisements (Quảng cáo)
Nên \(\widehat {DEB} = {90^0} \Rightarrow DE \bot BC\)
Mặt khác \(AH \bot BC\,\,\left( {gt} \right)\) do đó DE // AH
\( \Rightarrow \) Tứ giác ADEH là hình thang
Lại có \( = {90^0}\,\,\left( {AH \bot BC} \right)\)
Vậy tứ giác ADEH là hình thang vuông.
c) Ta có \(BE = BA\,\,\left( {gt} \right) \Rightarrow \Delta BAE\) cân tại B.
Mà BD là tia phân giác của góc B. Do đó BD là đường cao của tam giác BAE.
\(\Delta BAE\) có AH, BD là hai đường cao cắt nhau tại I \( \Rightarrow I\) là trực tâm của tam giác BAE.
\( \Rightarrow EF\) là đường cao của tam giác BAE
\( \Rightarrow EF \bot AB\)
Mà \(AC \bot AB \Rightarrow EF//AC\)
Vậy tứ giác ACEF là hình thang.
Mà \(\widehat {CAF} = {90^0}\). Do đó tứ giác ACEF là hình thang vuông.
