Bài tập 3 trang 103 Tài liệu dạy – học Toán 8 tập 1, Tứ giác ABCD có góc ngoài đỉnh A bằng 65 độ, góc ngoài đỉnh B bằng 100 độ, góc ngoài đỉnh C bằng 60 độ. Tính góc ngoài...

Tứ giác ABCD có góc ngoài đỉnh A bằng 65^o, góc ngoài đỉnh B bằng 100^o, góc ngoài đỉnh C bằng 60^o. Tính góc ngoài đỉnh D.

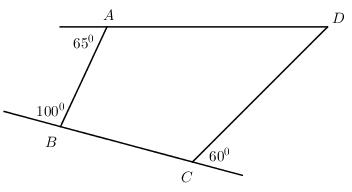
Ta có \(\widehat {BAD} + {\widehat A_{ngoai}} = {180^0}\) (hai góc kề bù)

Do đó : \(\widehat {BAD} + {65^0} = {180^0} \Rightarrow \widehat {BAD} = {180^0} - {65^0} = {115^0}\)

\(\widehat {ABC} + {\widehat B_{ngoài}} = {180^0}\) (hai góc kề bù)

Do đó : \(\widehat {ABC} + {100^0} = {180^0} \Rightarrow \widehat {ABC} = {180^0} - {100^0} = {80^0}\)

\(\widehat {BCD} + {\widehat C_{ngoài}} = {180^0}\) (hai góc kề bù)

Do đó : \(\widehat {BCD} + {60^0} = {180^0} \Rightarrow \widehat {BCD} = {180^0} - {60^0} = {120^0}\)

Tứ giác ABCD có \(\widehat {BAD} + \widehat {ABC} + \widehat {BCD} + \widehat {ADC} = {360^0}\)

Do đó \({115^0} + {80^0} + {120^0} + \widehat {ADC} = {360^0} \Rightarrow \widehat {ADC} = {360^0} - \left( {{{115}^0} + {{80}^0} + {{120}^0}} \right) = {45^0}\)

Ta có \({\widehat D_{ngoài}} + \widehat {ADC} = {180^0}\) (hai góc kề bù)

Do đó \({\widehat D_{ngoài}} + {45^0} = {180^0} \Rightarrow {\widehat D_{ngoài}} = {180^0} - {45^0} = {135^0}\)

Vậy góc ngoài đỉnh D bằng 135⁰