Advertisements (Quảng cáo)
Cho tam giác ABC cân tại A, các đường phân giác BD, CE \((D \in AC,E \in AB)\) .
a) Chứng minh rằng ED // BC.
b) Chứng minh rằng BEDC là hình thang cân có đáy nhỏ bằng cạnh bên.
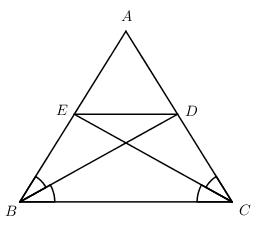
a) Ta có \(\widehat {ABD} = \widehat {DBC} = {{\widehat B} \over 2}\) (BD là tia phân giác của \(\widehat B\))
\(\widehat {ACE} = \widehat {ECB} = {{\widehat C} \over 2}\) (CE là tia phân giác của \(\widehat C\)), \(\widehat B = \widehat C\) (\(\Delta ABC\) cân tại A)
Suy ra \(\widehat {ABD} = \widehat {DBC} = \widehat {ACE} = \widehat {ECB}\)
Xét \(\Delta ACE\) và \(\Delta ABD\) ta có :
\(AC = AB\) (\(\Delta ABC\) cân tại A) ;
\(\widehat A\) chung ;
\(\widehat {ACE} = \widehat {ABD}\) (chứng minh trên)
Xét \(\Delta ACE = \Delta ABD\,\,\left( {g.c.g} \right) \Rightarrow AE = AD\) (hai cạnh tương ứng)
\( \Rightarrow \Delta AED\) cân tại A \( \Rightarrow \widehat {AED} = {{{{180}^0} – \widehat A} \over 2}\)
Mà \(\widehat {ABC} = {{{{180}^0} – \widehat A} \over 2}\) (\(\Delta ABC\) cân tại A). Nên \(\widehat {AED} = \widehat {ABC}\)
Mà \(\widehat {AED}\) và \(\widehat {ABC}\) là hai góc đồng vị.
Do đó ED // BC.
b) Vì ED // BC nên tứ giác BEDC là hình thang.
Mà \(\widehat {EBC} = \widehat {DCB}\) (\(\Delta ABC\) cân tại A). Do đó tứ giác BEDC là hình thang cân)
Ta có : \(\widehat {EBD} = \widehat {DBC}\) (hai góc so le trong và ED // BC)
\( \Rightarrow \widehat {EBD} = \widehat {EDB} \Rightarrow \Delta EBD\) cân tại E \( \Rightarrow BE = ED\).
Vậy tứ giác BEDC là hình thang cân có đáy nhỏ bằng cạnh bên.