Cho tam giác ANC nhọn. Gọi M, N, P lần lượt là trung điểm của AB, AC, BC. Kẻ đường cao AH. Chứng minh rằng tứ giác MNPH là hình thang cân.
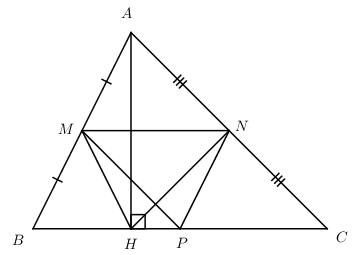
Xét tam giác ABC ta có:
M là trung điểm của AB (gt) ;
N là trung điểm của AC (gt) ;
\( \Rightarrow MN\) là đường trung bình của tam giác ABC \( \Rightarrow MN//BC\)
\( \Rightarrow \) Tứ giác MNPH là hình thang.
Xét tam giác ABC ta có :
Advertisements (Quảng cáo)
M là trung điểm của AB (gt) ;
P là trung điểm của BC
\( \Rightarrow MP\) là đường trung bình của tam giác ABC \( \Rightarrow MP = {1 \over 2}AC\)
\(\Delta ACH\) vuông tại H có HN là trung tuyến (N là trung điểm của AC)
\( \Rightarrow NH = {1 \over 2}AC\). Mà \(MP = {1 \over 2}AC\,\,\left( {cmt} \right)\)
\( \Rightarrow NH = MP\)
Hình thang MNPH (MN//PH) có \(MP = NH\) nên là hình thang cân.
Nhận xét : cần bổ sung thêm \(AB < AC\)