
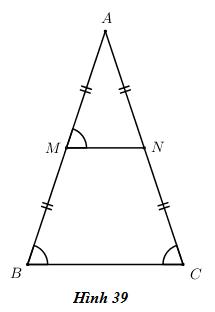
Cho tam giác ABC cân tại A (h.39). Gọi M, N lần lượt là trung điểm của AB, AC. Chứng minh rằng tứ giác MNCB là hình thang cân.

Tam giác ABC cân tại A (gt) \( \Rightarrow \widehat B = \widehat C,\,\,AB = AC\)
Do đó \(\widehat B = {{{{180}^0} - \widehat A} \over 2}\)
Mặt khác \(AM = {{AB} \over 2}\) (M là trung điểm của AB)
Và \(AN = {{AC} \over 2}\) (N là trung điểm của AC)
Advertisements (Quảng cáo)
Nên \(AM = AN \Rightarrow \Delta AMN\) cân tại A \( \Rightarrow \widehat {AMN} = \widehat {ANM}\).
Nên \(\widehat {AMN} = {{{{180}^0} - \widehat A} \over 2}\).
Ta có \(\widehat B = \widehat {AMN}\,\,\left( { = {{{{180}^0} - \widehat A} \over 2}} \right);\,\,\widehat B\) và \(\widehat {AMN}\) đồng vị \( \Rightarrow MN//BC\)
\( \Rightarrow \) Tứ giác MNCB là hình thang.
Mà \(\widehat B = \widehat C\) (\(\Delta ABC\) cân tại A)
Vậy tứ giác MNCB là hình thang cân.
