Advertisements (Quảng cáo)
Cho hình chữ nhật ABCD (AD<AB). Vẽ AH vuông góc với BD tại H.
a) Chứng minh rằng \(\Delta HAD \sim \Delta ABD\) .
b) Biết AB = 20 cm, AD = 15 cm. Tính độ dài các cạnh BD, AH.
c) Chứng minh rằng \(A{H^2} = HD.HB\) .
d) Trên tia đối của tia DA lấy điểm E sao cho DE < AD. Vẽ EM vuông góc với BD tại M. EM cắt AB tại O. Vẽ AK vuông góc với BE tại K. vẽ AF vuông góc với OD tại F. Chứng minh ba điểm H, F, K thẳng hàng.
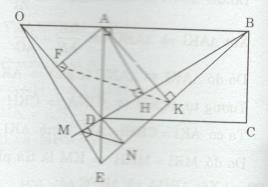
a) Xét ∆HAD và ∆ABD có: \(\widehat {ADH}\) (chung) và \(\widehat {AHD} = \widehat {DAB}( = 90^\circ )\)
Do đó \(\Delta HAD \sim \Delta ABD(g.g)\)
b) ∆ABD vuông tại A có:
\(B{D^2} = A{B^2} + A{D^2}\) (định lí Py-ta-go)
\(\eqalign{ & \Rightarrow B{D^2} = {20^2} + {15^2} = 625\cr& \Rightarrow BD = 25(cm) \cr & \Delta HAD \sim \Delta ABD \Rightarrow {{HA} \over {AB}} = {{AD} \over {BD}} \cr & \Rightarrow {{HA} \over {20}} = {{15} \over {25}}\cr& \Rightarrow HA = {{20.15} \over {25}} = 12(cm) \cr} \)
c) Xét ∆ADH và ∆AHB có:
\(\widehat {AHD} = \widehat {AHB}( = 90^\circ )\) và \(\widehat {DAH} = \widehat {ABH}\) (cùng phụ với góc ADH)
Do đó \(\Delta ADH \sim \Delta BAH(g.g) \)
\(\Rightarrow {{AH} \over {BH}} = {{DH} \over {AH}} \)
\(\Rightarrow A{H^2} = HD.HB\)
Advertisements (Quảng cáo)
d) Gọi N là giao điểm của OD và EB
∆EOB có EA, BM là hai đường cao cắt nhau tại D
=> D là trực tâm của tam giác EOB
=> ON là đường cao của tam giác EOB \( \Rightarrow ON \bot BE\)
Mà \(AK \bot BE \Rightarrow ON//AK\)
Xét ∆NOB có: ON // AK \( \Rightarrow {{BK} \over {BN}} = {{BA} \over {BO}}\) (định lí Thales)
Mặt khác \(AH \bot BM,OM \bot BM \Rightarrow AH//OM\)
Xét ∆MOB có: AH // OM \( \Rightarrow {{BH} \over {BM}} = {{BA} \over {BO}}\)
Xét ∆BMN có: \({{BK} \over {BN}} = {{BH} \over {BM}}\left( { = {{BA} \over {BO}}} \right) \Rightarrow HK//MN\) (định lí Thales đảo)
Xét ∆MDE có: AH // ME \( \Rightarrow {{DH} \over {DM}} = {{DA} \over {DE}}\) (hệ quả của định lí Thales)
Xét ∆NDE có: AF // NE \( \Rightarrow {{DF} \over {DN}} = {{DA} \over {DE}}\) (hệ quả định lí Thales)
Xét ∆DHF và ∆DMN có: \(\widehat {HDF} = \widehat {MDN}\) (đối đỉnh), \({{DH} \over {DM}} = {{DF} \over {DN}}\left( { = {{DA} \over {DE}}} \right)\)
Do đó \(\Delta DHF \sim \Delta DMN(c.g.c) \)
\(\Rightarrow \widehat {DHF} = \widehat {DMN} \Rightarrow HF//MN\)
Ta có HK // MN và HF // MN => HK, HF trùng nhau (tiên đề Ơ-clit)
Vậy H, F, K thẳng hàng