
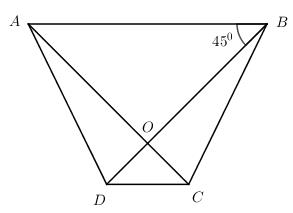
Cho hình thang cân ABCD (AB//CD) có \(\widehat {DBA} = {45^o}\) . Gọi O là giao điểm của AC và BD.
a) Chứng minh rằng tam giác AOB là tam giác vuông cân.
b) Chứng minh rằng tam giác DOC vuông cân.

a) Xét \(\Delta ABD\) và \(\Delta ABC\) ta có:
AB là cạnh chung ;
\(AD = BC\) (ABCD là hình thang cân) ;
\(\widehat {ABD} = \widehat {BAC}\) (ABCD là hình thang cân)
Advertisements (Quảng cáo)
Do đó \(\Delta ABD = \Delta BAC\,\,\left( {c.g.c} \right) \Rightarrow \widehat {ABD} = \widehat {BAC}\) (hai góc tương ứng)
Mà \(\widehat {ABD} = {45^0}\) nên \(\widehat {BAC} = {45^0}\).
\(\Delta OAB\) có \(\widehat {AOB} + \widehat {BAC} + \widehat {ABO} = {180^0}\)
\(\eqalign{ & \Rightarrow \widehat {AOB} + {45^0} + {45^0} = {180^0} \cr & \Rightarrow \widehat {AOB} = {180^0} - \left( {{{45}^0} + {{45}^0}} \right) = {90^0} \cr} \)
\( \Rightarrow \Delta AOB\) vuông tại O mà \(\widehat {ABO} = \widehat {OAB}\,\,\left( { = {{45}^0}} \right)\)
Vậy \(\Delta AOB\) vuông cân tại O.
b) Ta có : \(\widehat {DOC} = \widehat {AOB}\) (hai góc đối đỉnh) \( \Rightarrow \widehat {DOC} = {90^0} \Rightarrow \Delta DOC\) vuông tại O.
Mà \(\widehat {ODC} = {45^0}\) (vì \(\widehat {ABO} = \widehat {ODC}\), 2 góc so le trong và AB // CD)
Do đó \(\Delta ODC\) vuông cân tại O.
